Ctrl+K

Interpolation techniques

2. Interpolation techniques#

  • Nearest Neighbor - Uses the nearest single data point

  • Linear interpolation - Uses the two closest data points and draws a line between them

  • Cubic spline - Uses more nearby data points and fits a piecewise cubic polynomial

2.1. Linear interpolation#

\(\frac{\Delta z}{\Delta x}\) is same between all points

Find the data point \((x,z)\) that falls between \((x_1,z_1)\) and \((x_2,z_2)\). The value \(z\) is unknown, but \(x\) is known and falls between \(x_1\) and \(x_2\).

\(\frac{z - z_1}{x - x_1} = \frac{z_2 - z_1}{x_2 - x_1 }\)

\(z_i = \frac{z_2 - z_1}{x_2 - x_1 }\left(x - x_1\right) + z_1\)

2.2. Interpolation in Python#

import numpy as np
import matplotlib.pyplot as plt

# From np.interp doc-String
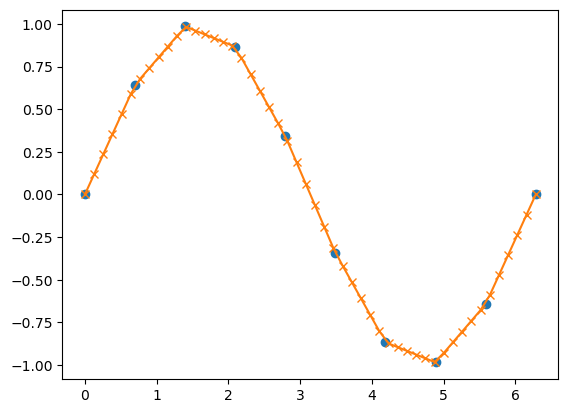
x = np.linspace(0,2*np.pi, 10)
y = np.sin(x)
xvals = np.linspace(0, 2*np.pi, 50)
yinterp = np.interp(xvals, x, y)

fig, ax = plt.subplots()
ax.plot(x,y,'o')
ax.plot(xvals,yinterp,'-x')

[<matplotlib.lines.Line2D at 0x1169a8990>]
_images/d1fdfda4a53fceacd304ad2da48cce1dc87b8ce763e99bc65996ccff1034b5ef.png 
from scipy.interpolate import interp1d
    
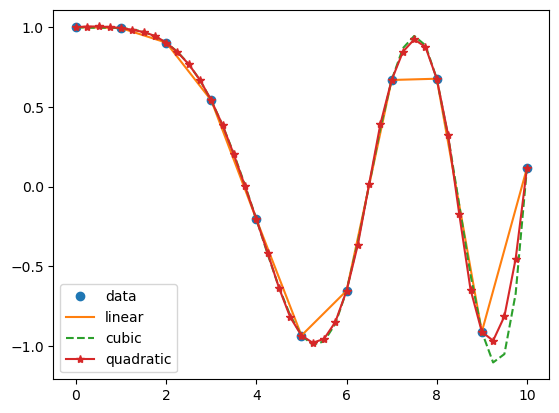
x = np.linspace(0,10,num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x,y)
f2 = interp1d(x,y, kind='cubic')
f3 = interp1d(x,y, kind='quadratic')


xnew = np.linspace(0,10, num =41, endpoint=True)
fig, ax = plt.subplots()
ax.plot(x,y,'o',xnew, f(xnew), '-', xnew, f2(xnew), '--',xnew,f3(xnew),'*-')
plt.legend(['data','linear','cubic','quadratic'],loc='best',numpoints = 1)

<matplotlib.legend.Legend at 0x116521a90>
_images/2c1224502068716f3775193ad24170d642a2c5e3be225bb87625823687535d27.png

2.3. Splines#

Originally, mechanical splines where used in boat building to draw a curved line through a set of points

Linear interpolation to design a hull would result in a an ugly inefficient boat design

Interactive spline example

Splines use data from not only the two nearest points, but also the the two points around the inner two.

  • “piecewise” fit -different polynomial for each interval between points

  • line : \( z = ax+b\) (two unkowns)

  • cubic : \(z = ax^3 + bx^2 +cx +d\) (four unknowns)

Pros#

  • smooth, not jagged: calculate derivatives at data points

  • Piecewise fit, i.e. the solution at one locations don’t affect the solution far away

  • Way better than fitting a polynomial to the entire function (ie if you have 8 data point and fit a 9th order polynomial)

Cons#

  • Closely spaced data points lead to “overshooting”

  • “Smoothing splines” help, but doesn’t represent data exactly

Contents